X-RAY RUNS: Apply for Beamtime
2017 Nov 1 - Dec 21
2018 Feb 7 - Apr 3
2018 Proposal/BTR deadline: 12/1/17
2018 Apr 11 - Jun 4
2018 Proposal/BTR deadline: 2/1/18
A long-term goal of the synchrotron radiation field has been to develop “perfect” hard x-ray synchrotron sources that would be capable of producing x-ray beams having full coherence and being diffraction limited. A fully coherent and diffraction limited beam would enable many new x-ray applications such as three-dimensional x-ray holography and nanoprobe microscopies, to name a few. Synchrotron x-ray beams are produced accelerating electrons to nearly the speed of light and passing them through arrays of magnetic devices called undulators. In order to increase the coherence and approach the diffraction limit it is necessary for the electrons in the beam to have as nearly the same energy and trajectory as possible. A common assumption has been that the ultimate process, namely the radiation produced by a single electron passing through an undulator, would necessarily produce fully coherent and diffraction limited radiation. Now Cornell physicist Ivan Bazarov has published a seminal paper[1] showing that this assumption is incorrect. The paper, while highly technical, has important implications for synchrotron radiation science. These apply to all synchrotron sources, including storage rings, energy recovery linacs and x-ray free electron lasers.
The highly collimated and spatially localized beams produced by modern accelerator-based x-ray sources are now approaching the Fourier transform limit, ΔxΔk≥1/2. Here, (Δx)^2 is the variance of the squared modulus of the wave function, |Ψ|^2, and the equality is achieved only when |ψ|^2 is Gaussian. To make contact between the wave description and the rays of geometrical optics, one makes the approximation Δk≈kΔθ. The uncertainty relation is then given by ΔxΔθ≳λ⁄4π, which is known as the “diffraction limit” and places a fundamental constraint on how small the phase-space area (the product of the size and the angular divergence) of an x-ray beam can become. Modern x-ray beams are also almost fully coherent – that is, the contrast of fringes in interference experiments is approaching unity. Note that coherence is a necessary but not a sufficient condition for being diffraction-limited.
In practice, the phase-space area of an x-ray beam is determined by the convolution of the radiation pattern of a single electron passing through an insertion device with the electron beam distribution. Since the equilibrium electron distribution in a storage ring is Gaussian and typically much broader than the single electron radiation pattern, Gaussian measures of the x-ray beam’s phase-space are widely used both to describe and to compare the properties of synchrotron x-ray sources. However, the Gaussian approximation breaks down near the diffraction limit. Bazarov’s paper[1] develops a general framework which accommodates non-Gaussian radiation patterns, non-Gaussian electron beam distributions, and partial coherence by using Wigner distribution function techniques originally developed for quantum mechanics. By calculating the radiation field in the far field and then propagating the Wigner distribution back to the source (see figure below), one obtains the phase-space distribution of a single electron passing through an undulator. Contrary to a widespread belief, the radiation pattern, though fully coherent, is not diffraction limited, (ϵx=2.7 λ⁄4π). The paper proposes and discusses the merits of novel figures of merit appropriate for comparing future x-ray sources that do not have Gaussian beams.
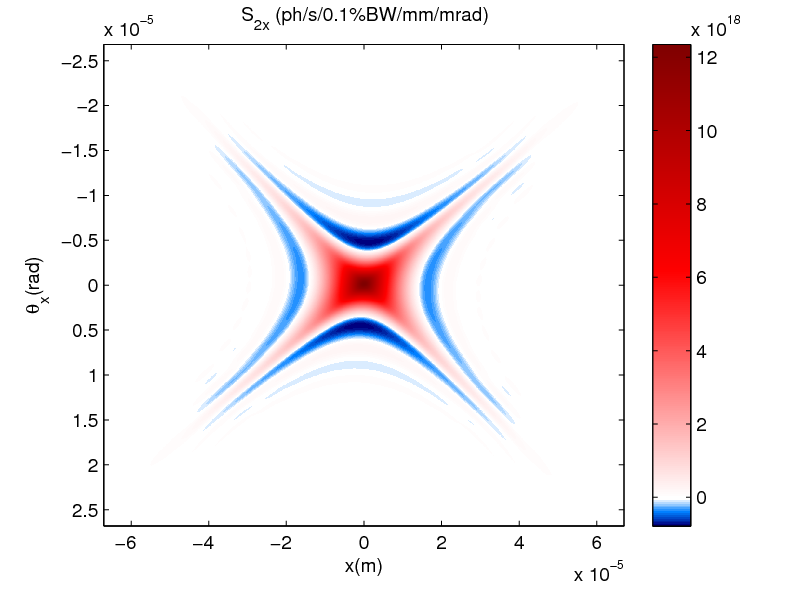
Phase space distribution for a planar undulator with Nu = 250 on resonance of the 1st harmonic at 8 keV photon energy.
Reference:
[1] Ivan V.
Bazarov; "Synchrotron Radiation Representation in Phase Space", Physical Review Special Topics - Accelerators and Beams 15 (5), 050703 (2012)
Notes:
Definition of Fourier transform used here:
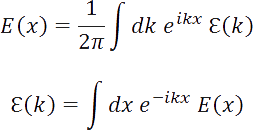
Normalized Gaussian wave packet:
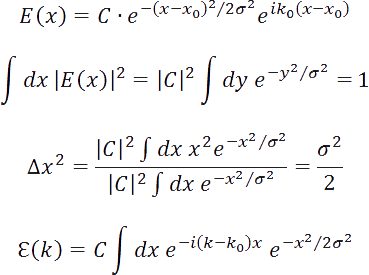
Submitted by: Ernie Fontes, CHESS, Cornell University
06/12/2012
