X-RAY RUNS: Apply for Beamtime
2017 Nov 1 - Dec 21
2018 Feb 7 - Apr 3
2018 Proposal/BTR deadline: 12/1/17
2018 Apr 11 - Jun 4
2018 Proposal/BTR deadline: 2/1/18

We all have loved to play with woodblocks at some point of our career. At first, we may have put block to block to create a square array as a base, and then we started the next layer. At this point an interesting question arises: do we put the first block on top of a bottom block, do we choose a brick-wall arrangement, or maybe put it on the junction of four underlying blocks to go for a pyramid? Now, what would happen, if we tried to build a block arrangement on the nanoscale? At this length scale, manual manipulation is obviously impossible, and we will have to turn to clever methods to direct the self-assembly of nanoscale building blocks. This means in context of our favorite Kindergarten activity: let’s throw all cubes back into the box, give it a good shake, and see what we get!
Recent experiments by Tobias Hanrath and co-workers at CHESS D1 station examined the self-assembly of cubic nanoparticles from a colloidal suspension dropped onto a silicon wafer. As the solvent in the thin film of the suspension evaporated, interfacial forces went into action. Van der Waals interactions at the interface between the substrate and the liquid gave rise to a beautiful square layer; this arrangement maximizes the interfacial contact with the substrate and neighboring nanocubes. Surprisingly, completely different arrangements of cubes formed at the liquid/air interface. Since the solvent likes to wet the nanoparticles, only some of their corners stuck out of solution. Interactions between neighboring cubes at the liquid/air interface resulted in the formation of a hexagonal layer – of cubic objects! This unusual ‘corner-up’ arrangement of cubes at the liquid/air interface imposed the structure of subsequent layers and led to the formation of a rhombohedral packing. This was the first discovery of two different types of superlattice symmetries formed at the solid/liquid and liquid/air interface within the same film. Moreover, the experiments showed that the relative fraction of cubes assembled ‘face-up’ at the substrate/liquid interface and ‘corner-up’ at the liquid/air interface could be tailored by adjusting the self-assembly conditions[1]. Interestingly, although the physical mechanisms differ, the orientation of nanocubes at interfaces is the same as for centimeter-sized cubes in water as shown in the Figure above.
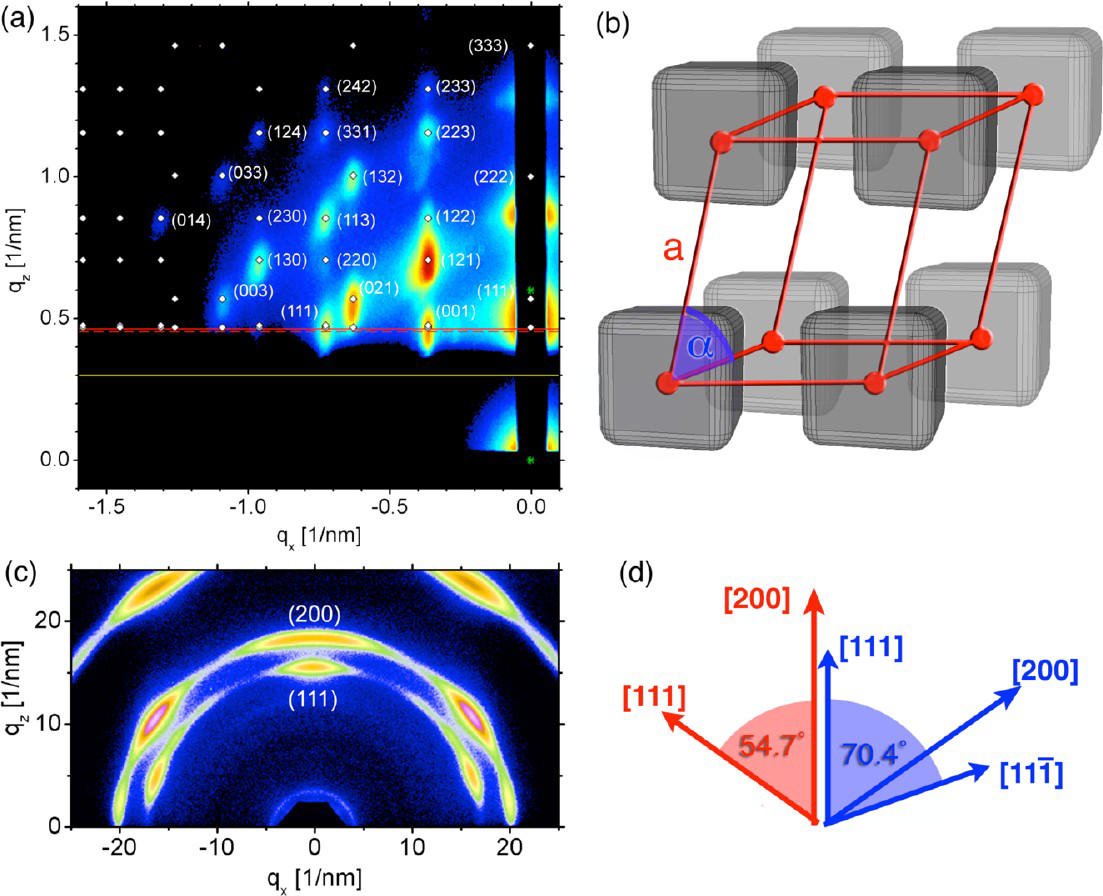
Figure 2: (a),(b): Rhombohedral
suplattice with a (111) orientation formed at the solution surface. (c): ): Diffraction from nanocubes showing both corners (111 reflections) and faces (200 reflections) parallel to the substrate. (d) shows, how other reflections are related to the reflections perpendicular to the substrate - all observed maxima on the PbS (111) and (200) Debye-Scherrer rings can be accounted for.
Cornell students Josh Choi and Kaifu Bian investigated the complex growth of simple PbS nanocubes in-situ with a combination of grazing incidence small- and wide-angle x-ray scattering. Small-angle scattering revealed the superlattice symmetry and orientation, wide-angle scattering the orientation of the nanocubes within the superlattices. Both techniques showed unambiguously the co-existence of both interface-induced nanocube orientations. The finding explains, why nanocubes superlattices do not form quite as readily as other superlattices – there is a significant competition of structures. As the most basic of all nanocrystal shapes, the nanocube orientation and lattice symmetry are very important for theoretical modeling, as well as understanding collective electronic, optical, and magnetic properties for the development of novel artificial materials.
Reference:
[1] Joshua J. Choi, Kaifu Bian, William J. Baumgardner, Detlef-M. Smilgies, and Tobias Hanrath; "Interface-Induced Nucleation, Orientational Alignment and Symmetry Transformations in Nanocube Superlattices", Nano Lett. 12, 4791–4798 (2012)
Submitted by: Detlef Smilgies, CHESS, Cornell University
10/29/2012
