X-RAY RUNS: Apply for Beamtime
2017 Nov 1 - Dec 21
2018 Feb 7 - Apr 3
2018 Proposal/BTR deadline: 12/1/17
2018 Apr 11 - Jun 4
2018 Proposal/BTR deadline: 2/1/18
Transverse or spatial coherence is one of the key metrics used to characterize the x-ray beams generated by 4th generation light sources. Full spatial coherence is highly sought after because as a light source approaches that level of perfection, new x-ray probes and techniques become possible such as coherent diffraction imaging (CDI), x-ray photon correlation spectroscopy (XPCS), as well as enabling efficient focusing by Fresnel lenses to create diffraction limited beam-waists. One of the simplest ways to start thinking about coherence is to realize that the x-ray beam produced by a single electron passing through an undulator is completely coherent. In practice, the finite size, angular divergence, and energy bandwidth of multi-particle electron bunches degrades the coherence. When the emittance ε is large relative to the diffraction limit, the coherence scales as ε-1. Qualitatively, one expects that as the emittance (size x divergence) of the electron beam becomes than smaller than the diffraction limit of a wave, λ/4π, the x-ray beam will become coherent.
Given the cost of building and operating low emittance, high energy 4th generation storage ring light sources, understanding the precise details of how the coherence of the x-ray beam behaves as the electron beam emittance approaches the diffraction limit is critically important. Cornell Faculty member Ivan Bazarov and his undergraduate student Andrew Gasbarro performed this calculation for radially symmetric beams in a recent paper published in the Journal of Synchrotron Radiation [1]. They find that the overall degree of coherence of the x-ray beam is more sensitive to the electron beam emittance than its bandwidth and that there is a dramatic, non-linear increase in the overall degree of coherence just as the electron beam emittance reaches the diffraction limit of the x-ray (figure 1). Therefore, to achieve a highly coherent x-ray source the accelerator needs to achieve an electron beam emittance less than or equal to the diffraction limit of the x-ray.
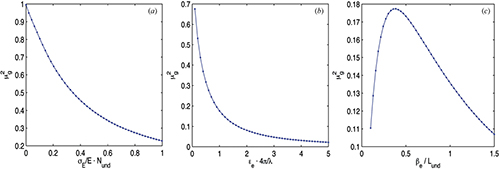
Figure 1: Coherence of x-ray beam vs. emittance.
References:
[1] Andrew Gasbarro and Ivan Bazarov, "Reduced forms of the Wigner distribution function for the numerical analysis of rotationally symmetric synchrotron radiation," Journal of Synchrotron Radiation 21(2), (2014).
Submitted by: Joel Brock, CHESS, Cornell University
03/13/2014
